
Un giorno, tempo fa, leggendo un forum di radioamatori, incappai in un collega che si chiedeva come facesse a funzionare una antenna a loop, dato che essa era in corto circuito. La cosa mi fece riflettere: perché invece non si stupiva che circolasse corrente nel dipolo che, essendo costituito da due fili collegati a nulla, era un un circuito aperto?
Elettrotecnica e radiotecnica
Quando si esamina il funzionamento di antenne e linee di trasmissione ci si scontra con delle apparenti contraddizioni con alcune leggi fisiche. Ad esempio, un ostacolo da superare sono certamente le leggi di Kirchhoff. Queste infatti prevedono che perché circoli corrente, il circuito deve essere chiuso.
Ma questo non è tutto: Kirchhoff dice anche che in ogni punto di un conduttore, in assenza di nodi, la corrente deve essere costante:
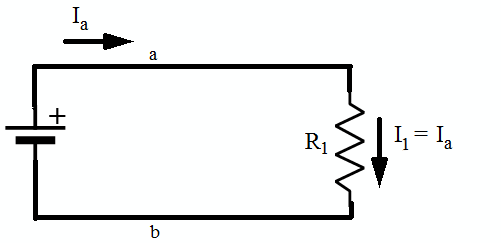
Perché la corrente possa assumere valori diversi, ci devono essere dei nodi in cui questa possa dividersi e circolare in più maglie:
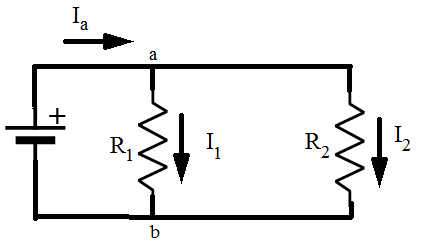
Eppure, come tutti i libri ci insegnano, i due fili del dipolo, non solo formano un circuito aperto, ma al loro interno la corrente circolante non è per niente costante come vorrebbe Kirchhoff, ma anzi essa è diversa in ogni punto, come il simulatore NEC ci mostra chiaramente:
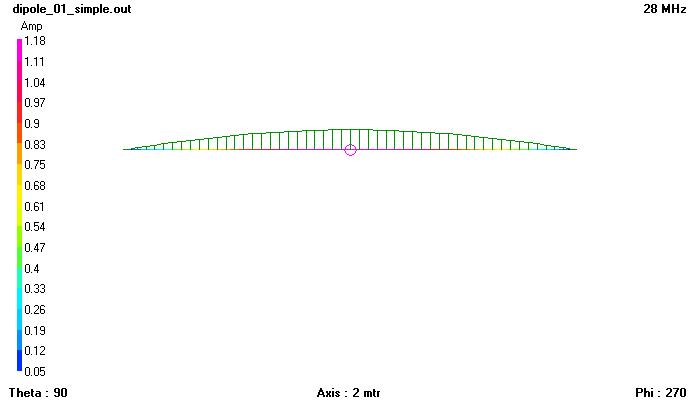
E quindi… Kirchhoff?
Perché le leggi di Kirchhoff continuino a valere anche in un dipolo, è necessario che si individuino dei componenti “invisibili” capaci di trasferire corrente, chiudendo il circuito e formando infiniti nodi.
Tali “componenti” in effetti esistono e sono realizzati dal near-field: quando una corrente scorre in un conduttore le cui dimensioni siano in ordini di grandezza della lunghezza d’onda, in un’area circostante ai conduttori stessi si forma un campo elettromagnetico chiamato near-field. Questo campo elettromagnetico fa due cose:
- consuma energia generando un altro campo elettromagnetico che lascia l’area per propagarsi all’infinito consentendoci di comunicare con stazioni lontane (far-field);
- ingenera altre correnti in tutti i conduttori che entrano nel suo raggio d’azione;
In particolare è il secondo punto che di fatto realizza gli infiniti collegamenti mancanti che “chiudono” il circuito del dipolo.
Nell’illustrazione che segue si vedono alcuni degli infiniti “componenti virtuali” che collegano i tre conduttori A, B e C:
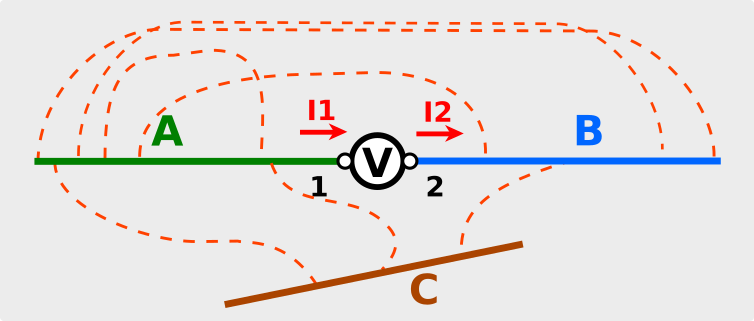
Notiamo che, grazie al near field, la corrente scorre anche nel conduttore C anche se non è fisicamente collegato a nulla.
Il near-field costituisce gli infiniti nodi che giustificano sia la circolazione di corrente che il fatto che in ogni punto dei fili fisici, la corrente sia sempre diversa di quella che scorre in altri punti.
Possiamo anche notare un fatto importante, mostrato dall’illustrazione seguente:
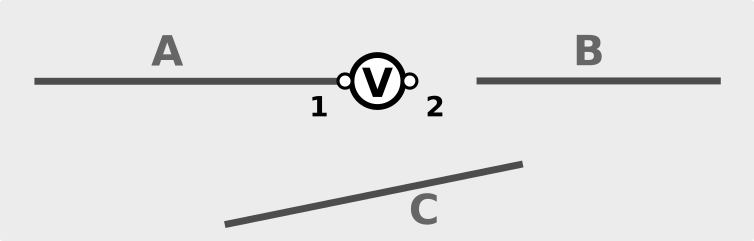
In quest’ultimo caso abbiamo gli stessi tre conduttori A, B e C, solo che ora B non è più collegato al generatore. In questo caso non circola corrente perché il generatore “V” è parte di un circuito aperto. Perché il circuito sia chiuso dal near-field è necessario che entrambi i poli del generatore siano collegati a conduttori capaci di partecipare alla generazione del near-field. Qui invece il conduttore B è sì in grado di partecipare al near-field, ma non ha la possibilità di ricondurre la corrente all’interno del morsetto 2 del generatore, che quindi risulta collegato al circuito per un solo polo. In questa illustrazione abbiamo realizzato una end-fed perfetta la quale, non chiudendo il circuito, non può funzionare.
L’impedenza
Gli infiniti collegamenti virtuali che sono realizzati dal near-field possono essere pensati come infinite impedenze (cioè componenti dotati di una parte resistiva ed una reattiva) che collegano i vari punti:
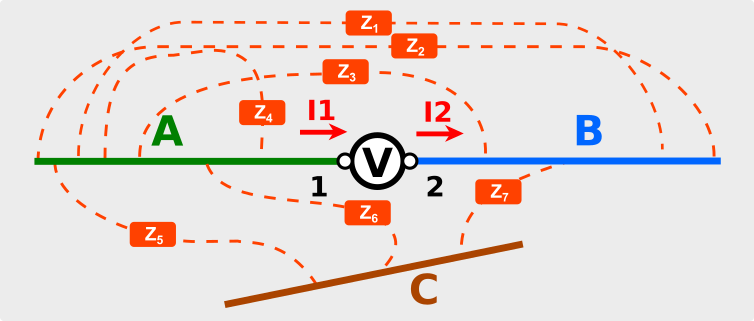
Queste impedenze, una volta combinate tra loro, formano l’impedenza finale “vista” dal generatore al suo punto di alimentazione:
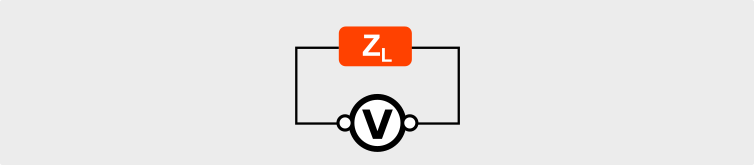
Notiamo anche che l’impedenza finale è condizionata anche dalla presente di altri conduttori non fisicamente collegati al generatore, come nel caso di C nell’illustrazione. Questo fatto è noto ai costruttori di Yagi, che sanno che avvicinando o allontanando gli elementi passivi possono variare l’impedenza dell’antenna.
La linea di trasmissione
Ora prendiamo il nostro dipolo, pieghiamone i fili e realizziamo una struttura come quella della figura successiva:
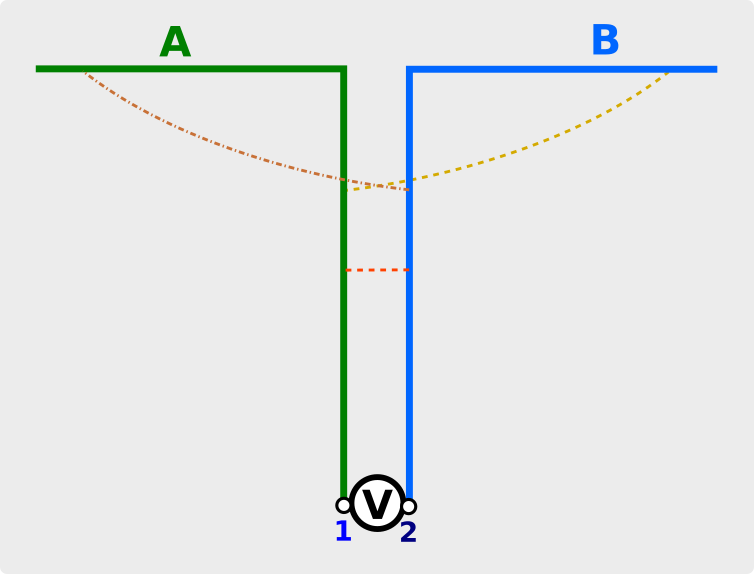
I due fili verticali paralleli molto vicini tra loro sono soggetti alle stesse leggi fisiche del dipolo visto in precedenza (figura 1). Questi fili, percorsi da corrente alternata ad alta frequenza, generano un near-field che cerca di interagire con gli oggetti circostanti. A differenza del dipolo, però, ognuno di questi fili è affiancato da un omologo filo simmetrico in cui scorre corrente identica e contraria. Per ogni interazione instaurata tra il filo di sinistra e qualche altro oggetto esisterà un’identica ma contraria interazione instaurata dal filo di destra. Il risultato è che i campi E/M generati da questi fili si annullano tra loro e i due elementi verticali non possono irradiare. Abbiamo realizzato una linea di trasmissione che non riesce a fare altro che non sia trasferire la potenza generata da “V” al dipolo soprastante.
Se osserviamo una simulazione realizzata con NEC, vediamo che le correnti sui due rami sono identiche in ogni punto:
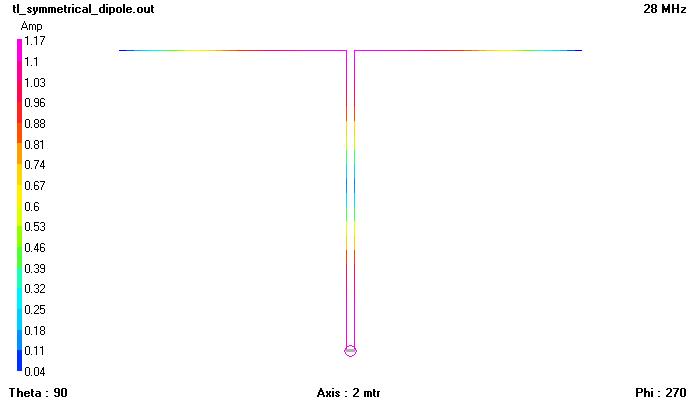
Adesso colleghiamo un altro filo al sistema in modo che la simmetria venga meno ed eseguiamo una simulazione con NEC-2:
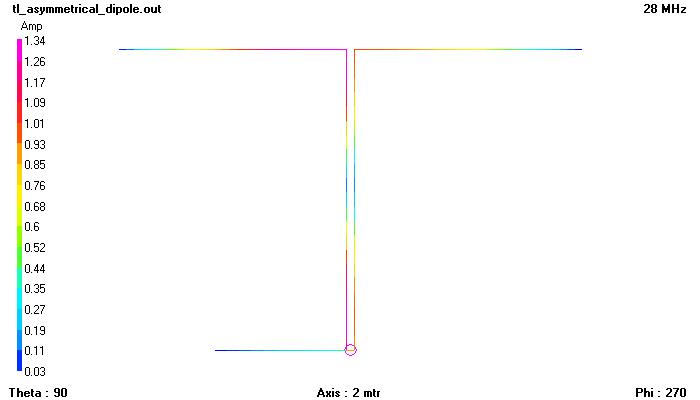
Come si vede chiaramente, nei due fili verticali la corrente non è più identica nei vari punti. Infatti il filo di destra può creare interazioni con il filo aggiuntivo che, data l’asimmetria, non sono speculari alle interazioni che può realizzare il filo di sinistra.
Pertanto la somma delle correnti sulla linea di trasmissione non è più nulla: la corrente risultante si chiama corrente di modo comune e crea un regolare near-field che irradia RF come qualunque altra parte radiante dell’antenna.
Il cavo coassiale
Il cavo coassiale, nonostante la sua diffusione universale, ha alcune caratteristiche peculiari molto interessanti che non sempre sono ben comprese da coloro che se ne servono.
Prendiamo una comune resistenza R e colleghiamola come carico al termine della nostra linea di trasmissione fatta con due fili e, per confronto, al termine di un cavo coassiale:
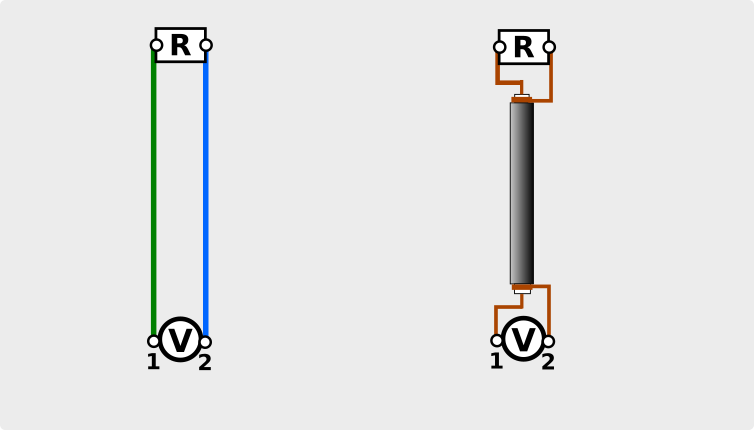
Come è facile intuire, nessuno dei due sistemi irradia RF. La potenza viene completamente assorbita dalla resistenza che la trasforma in calore.
Adesso però introduciamo una piccola variazione sul tema. Inseriamo un ulteriore filo che crei un’asimmetria e vediamo cosa succede:
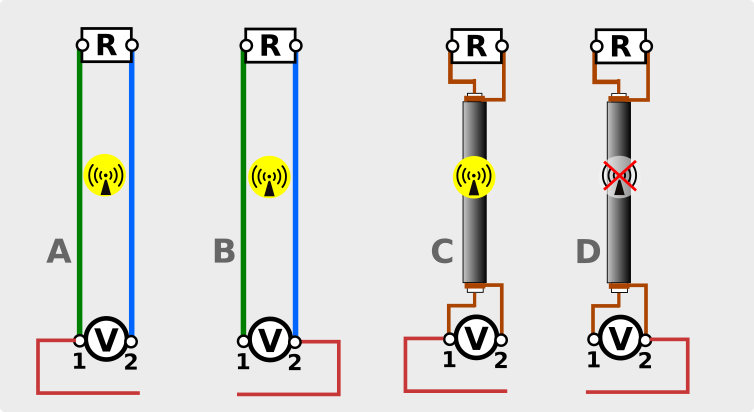
Tre delle quattro combinazione sopra illustrate, A, B, e C, irradiano RF: i due conduttori che costituiscono ciascuna linea iniziano ad interagire in maniera asimmetrica con il filo aggiunto, creando uno sbilanciamento delle relative correnti e causando la comparsa di correnti di modo comune. In particolare, i casi A e B sono gli stessi già visti in figura 3.
Il caso D invece, quello in cui il filo aggiuntivo è stato collegato nello stesso morsetto in cui è collegata la calza del coassiale, fa storia a sé perché non irradia.
Benché così esposto sembri un caso eccezionale, esso rappresenta invece la situazione che normalmente tutti sperimentiamo quando trasmettiamo in un carico fittizio: in questo caso il “filo aggiuntivo” non è altro che la scatola metallica dell’apparato e le altre cose ad essa collegate.
Questo semplice esperimento illustra la casistica D dimostrando l’assenza di irradiazione:

Il caso C invece è analogo quello dell’antenne end-fed, dove un pezzo di filo viene collegato al centrale del coassiale (eventualmente con trasformatore di impedenza). Non importa in che punto del centrale sia collegato: che sia all’inizio o alla fine del cavo, la presenza di tale filo aggiuntivo fa sì che tutto il sistema (filo e coassiale) irradi:

L’esistenza del caso D è la ragione fondamentale per cui il cavo coassiale si definisce sbilanciato mentre la linea bifilare si definisce bilanciata.
Notiamo che in questi esempis:
- il generatore del nostro esempio ha due morsetti numerati 1 e 2 perfettamente equivalenti; non li ho denominati “polo caldo” e “polo freddo”, come spesso vengono descritti, facendo pensare che abbiano caratteristiche diverse;
- non c’è la Terra: la Terra, nonostante sia sempre chiamata in causa in ogni descrizione tra i sistemi bilanciati e sbilanciati, non è il protagonista ma solo un attore che può anche non esserci;
Come funziona il coassiale
Quando una linea di trasmissione viene configurata in forma coassiale, a causa della particolare geometria, i campi elettromagnetici che si formano sono interamente concentrati nel dielettrico che si trova tra il centrale e la calza. L’energia viene trasportata quasi totalmente dal campo E/M nel dielettrico e le correnti che si formano sui conduttori sono localizzate sulla superficie esterna del conduttore centrale e quella interna della calza.
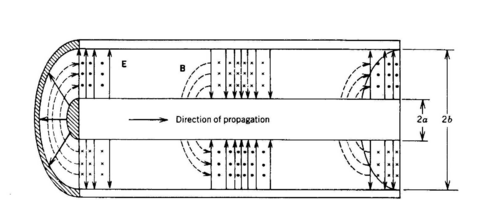
Essendo il campo E/M completamente confinato all’interno, non esiste campo E/M all’esterno: pertanto esso non può interagire con elementi esterni e “chiudere il circuito” in maniera alternativa.
Dal punto di vista esterno, invece, il coassiale è una specie di “tubo metallico” collegato elettricamente alla scatola dell’apparato. Eventuali correnti eventualmente indotte esternamente su di esso scorreranno, per via dell’effetto pelle, sulla superficie esterna dello stesso senza interagire con quelle presenti all’interno. In pratica, contenitore e calza del coassiale formano un unico involucro che incorpora tutti i componenti, qui rappresentato in blu:
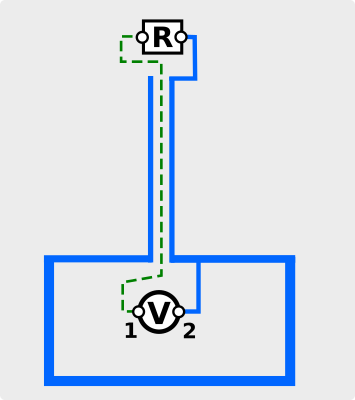
Tutto questo metallo mostrato in blu potrebbe essere un’ottima antenna come qualunque altro oggetto metallico di pari dimensioni. Esso non irradia semplicemente perché manca un’elemento radiante “verde” collegato al morsetto 1 capace di chiudere il circuito. In questo frangente siamo nella situazione di figura 2, dove solo un morsetto è collegato ad un elemento radiante e quindi il “circuito RF” non si chiude.
Walt Maxwell W2DU, nel suo celebre manuale intitolato “Reflections”, illustra il funzionamento del cavo coassiale mostrando un circuito equivalente. Ecco la sua illustrazione:
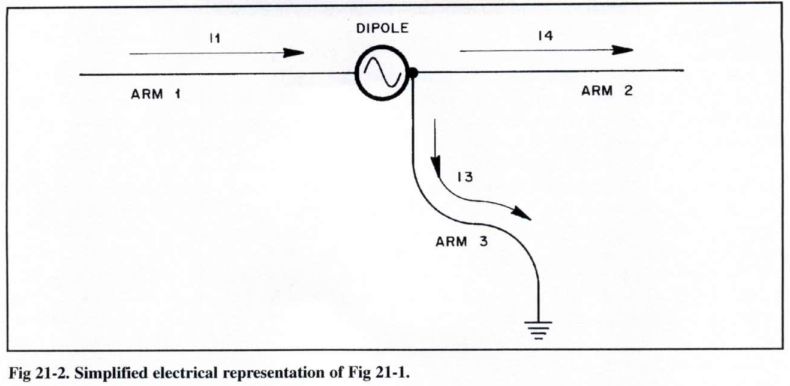
Maxwell spiega che collegare un generatore RF alla base di un cavo coassiale è, attenuazione a parte, come mettere il generatore direttamente al carico e collegare la sola calza ad uno dei poli. Volendo rappresentare una radio collegata ad un carico fittizio secondo il modello di W2DU avremmo che:
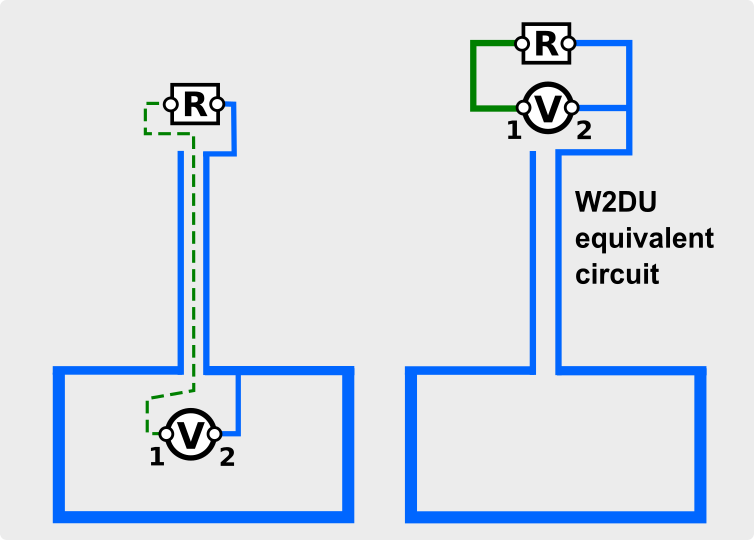
Come si vede dal circuito equivalente di W2DU, il coassiale non irradia quando collegato ad un carico fittizio perché l’enorme mole potenzialmente radiante blu collegata al morsetto 2 non è coadiuvata da alcun elemento radiante collegato al morsetto 1 (verde) che consenta di formare un “circuito RF” chiuso tramite near-field. La corrrente può solo circolare nella resistenza R e così effettivamente fa.
Un esperimento sul coassiale
La differenza tra un cavo coassiale (sbilanciato) ed uno bifilare (bilanciato) è che nel cavo coassiale usato come linea di trasmissione, solo la calza può agire da elemento radiante. Questo consente di collegare la calza alla scatola della radio, alla messa a terra e a qualunque altro oggetto senza preoccuparsi della simmetria della linea di trasmissione, tanto il centrale non può partecipare alla formazione di una antenna indesiderata.
Possiamo vedere questo comportamento con un semplice esperimento.
Nell’esperimento illustrato nel video si ha dapprima una normale connessione coassiale ad un carico fittizio. Quindi, la connessione viene modificata in modo che da un certo punto in poi, il centrale e calza siano invertiti. Ecco lo schema che rappresenta i due esperimenti:
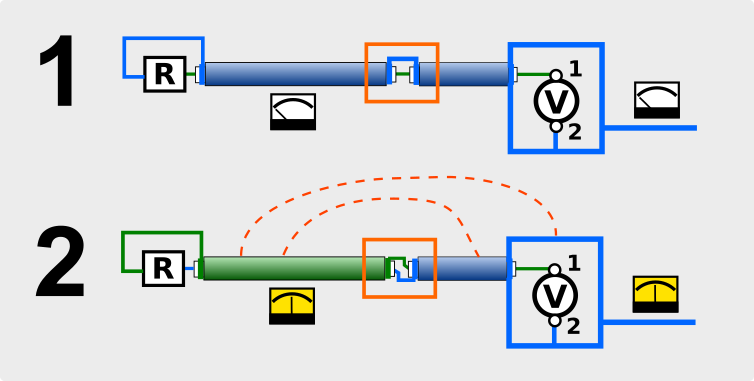
Il caso n.1 costituisce una normale connessione coassiale. Il ramo blu ha tanta “superficie radiante”, mentre il ramo verde non ne ha per niente: per questo la “antenna” non è completa e il sistema non irradia.
Se però ad un certo punto invertiamo la connessione del coassiale, otteniamo che la calza, che può essere elemento radiante, serve il “ramo verde” del circuito. Abbiamo quindi ottenuto un’antenna radiante costituita dalla calza del coassiale a sinistra per il “ramo verde” e dalla calza del coassiale a destra, dalla scatola e dal corto filo collegato alla scatola per quanto riguarda il “ramo blu”. Questa antenna si pone in parallelo al carico fittizio e si divide l’energia secondo le normali leggi di Ohm e Kirchhoff.
Le correnti di modo comune
Come abbiamo visto, una linea di trasmissione può irradiare solo in presenza di correnti di modo comune: se il totale delle correnti che scorrono nei conduttori della linea non si azzera completamente, la parte rimanente irradia. Che sul coassiale le correnti di modo comune scorrano sulla superficie esterna del coassiale mentre quelle differenziali scorrano sul centrale e all’interno della calza è solo un dettaglio tecnico del funzionamento del coassiale: non c’è nessuna necessità che le correnti di modo comune scorrano su conduttori diversi da quelli delle correnti differenziali.
Ad esempio, sulle linee bilanciate, avremo una corrente che scorre su un filo e un’altra che scorre sull’altro: il fatto che vi siano “correnti differenziali” o “correnti di modo comune” è solo una convenzione logica. Quando vediamo che la somma delle due correnti non si azzera, chiamiamo la quota di corrente che non si è azzerata “corrente di modo comune”.
Per semplicità di ragionamento e di calcolo possiamo considerare le due correnti (differenziali e di modo comune) come due entità separate che convivono sullo stesso cavo, ma non è necessario che esse siano realmente fisicamente separate.
Fine prima parte


Bello. Ma ne ero sicuro. Aspetto la seconda…
IT9FGH, Complimenti per la chiarissima esposizione, che condivido in tutto tranne che nel seguente punto:- “”Il caso C invece è analogo quello dell’antenne end-fed, dove un pezzo di filo viene collegato al centrale del coassiale (eventualmente con trasformatore di impedenza). Non importa in che punto del centrale sia collegato: che sia all’inizio o alla fine del cavo, la presenza di tale filo aggiuntivo fa sì che tutto il sistema (filo e coassiale) irradi: “”
Personalmente uso una End Fed antenna, con interposto Remoto ATU (antenna tuning Unit) tra la fine del cavo coassiale ad il piede dell’antenna. Posso garantire che in questa configurazione il mio sistema d’antenna non irradia. Tutt’altra cosa è una End Fed antenna non coniugata alla giusta impedenza e non in risonanza alla freq. emissione.
Rinnovo i miei complimenti all’autore del post che ho condiviso su “SICILIA RADIO CLUB (nel web) “” it9fgh@alice.it
Non deludi mai le aspettative, ottimo articolo,scritto per essere utile, capito ed assimilato da tutti.
73 de IU2FZA ex IW2MUR
Ho letto quest’articolo e anche altri tuoi articoli, ho anche iniziato a leggere Reflections o lo Another look at reflections originario di Walter Maxwell. Tirando le somme sembrerebbe che il cavo coassiale rischia sempre di irradiare, praticamente anche con una ground plane. Secondo il modello di W2DU, infatti, lo stilo di una ground plane al posto del carico fittizio nella figura relativa al menzionato modello basterebbe a mettere la superficie esterna dello schermo del cavo coassiale in condizione di irradiare. Non credo insomma che la presenza dei radiali potrebbe cambiare qualcosa a riguardo. Abbiamo sempre sbagliato anche quando tra una tranquilla ground plane commerciale e il connettore del cavo non interponevamo alcun dispositivo che potesse isolare la superficie esterna del cavo? Insomma col cavo coassiale non se ne esce mai se lo si collega direttamente all’antenna? È davvero questa la conclusione a cui intendevi arrivare?
Ciao Andrea.
Non è mai una questione di “se”, è sempre una questione di “quanto”.
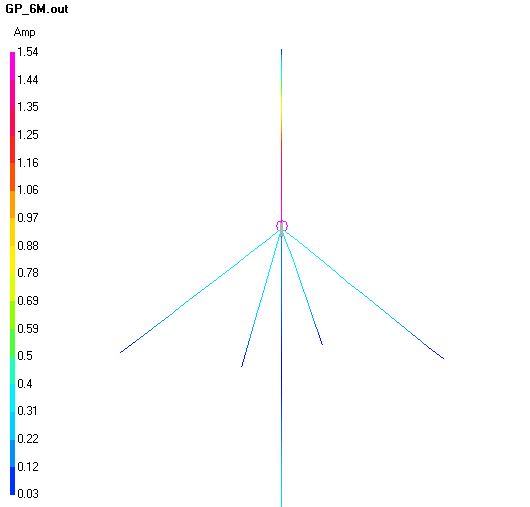
La calza del cavo coassiale si comporta come un componente dell’antenna e su questo non ci piove. Non è detto però che su tutti i componenti di un’antenna si sviluppi la stessa corrente. In particolare, nel caso della GP, il coassiale compete con i radiali nell’ottenere la sua quota di corrente. Infatti nel punto di alimentazione, la corrente che viene immessa nell’elemento verticale è uguale e contraria a quella che viene immessa nei radiali e nella calza. I radiali sono lunghi 1/4 d’onda e favoriscono lo scorrimento di corrente a quella frequenza. Lo stesso fenomeno lo puoi vedere con un fan dipole: in base alla frequenza, la corrente scorre sul dipolo la cui lunghezza è 1/2 onda ed ignora gli altri.
Il coassiale, a differenza dei radiali, è un elemento di lunghezza random. Pertanto, mentre lo stilo verticale riceve per intero la sua quota di corrente, per l’altro ramo la corrente deve essere divisa sui vari radiali e sulla calza random; quindi già la corrente è ridotta perché distribuita su tanti elementi, ma pure il coassiale non è (se non in casi molto sfortunati) di una lunghezza elettrica di 1/4 d’onda. Per questo la GP classica funziona (e non per niente si collega la calza ai radiali e non al centrale).
Stesso fenomeno capita alimentando un filo lungo 1/2 onda su un polo e di lunghezza qualunque sull’altro: la corrente si sviluppa quasi completamente sul filo lungo 1/2 onda e pochissimo sull’altro.
Nel caso di queste antenne, l’effetto “balun” è ottenuto intrinsecamente per il modo in cui sono costruite. Infatti capita che tentando di accordare tali antenne su altre bande si abbiano evidenti rientri: infatti, se un’antenna ha certe caratteristiche peculiari (es. è lunga mezz’onda), cambiando frequenza non le ha più e così viene meno l’effetto “balun automatico”.
Ciaoo
Davide
Ho capito che il disegno rappresenta una mappa di distribuzione della corrente (è evidente dalla colorazione che il ventre di corrente sia al centro), ma debbo confessare che non ho ancora capito cosa lo produce e in base a cosa (sul blog o non ho cercato bene o non viene spiegato). Due perplessità:
In quel random non ci potrebbe facilmente capire un multiplo dispari di un quarto di lunghezza d’onda che eleverebbe il cavo ad un livello più vicino a quello dei radiali per quanto riguarda il prendersi una quota di corrente?
Alimentare un conduttore lungo mezza lunghezza d’onda ad un estremo non comporta necessariamente l’utilizzo di un adattatore d’impedenza? Una Ringo sarebbe fatta proprio così… Mi vuoi dire che è garantito che sotto ad una verticale mezz’onda alimentata tramite autotrasformatore il cavo se ne stia buono senza entrare in gioco come problema? 😉
Addendum
1) capire —> finire
2) I tag html per una lista non ordinata non possono funzionare, ma si sarà capito quali siano i due punti… 😉
Buondi Davide, bellissime trattazioni,complimenti.
E se il choke lo mettessimo lungo il coax? 73’s.Loris.
È quel che ho fatto io, sia sopra che in prossimità degli apparecchi. Però non ho mai realizzato lo strumento usato sovente da Davide, quindi non so dire quanto i miei choke siano efficaci. Posso dire solo che offrivano una robusta induttanza-serie sullo schermo anche sulle frequenze più basse. Ma per dire che fosse abbastanza dovrei misurare e ancora non l’ho fatto.
73 de IK0RNT Andrea